Gompertz-Makeham law of mortality

Gompertz-Makeham Law of Mortality, where μ(x) indicates mortality rate, α and β are constants, and γ represents factors unrelated to age which contribute to mortality.

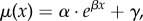
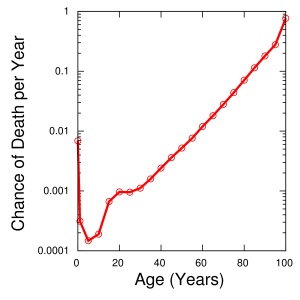
The Gompertz-Makeham law of mortality is an equation which shows the increase in mortality rates for organisms as they age.

The Gompertz law is based on the observation that biological processes in the body change with aging, resulting in a higher risk for illnesses and ultimately death. The mortality rate does not grow linearly, but exponentially, meaning that it continues to accelerate with age. This exponential change is observed virtually universally, both across regions and time.

History

The law's predecessor, Gompertz's law (written as μ(x)=αe^βx), was formulated by an actuary named Benjamin Gompertz, and published in an 1825 paper. He wished to help others in his profession calculate the most profitable rates at which to sell annuities to purchasers of various ages. He had observed that mortality rate appeared to increase exponentially over the adult human lifespan. As his model fit reasonably well with observed data, it was quickly adopted by actuaries and demographers for their own work. The law in its modern form appeared with a modification to Gompertz’s law (generally attributed to William Makeham) to account for age-independent factors affecting mortality rate (which Makeham himself had speculated might improve its accuracy).

Description

The Gompertz-Makeham law of mortality describes the risk of dying, which the graph depicts to exponentially increase between 30 and 80 years of age. Data from the US National Vital Statistics Report in 2003.

When solved for mortality rate, the law can be written as μ(x)=αe^βx+γ, where "μ(x)" represents mortality rate at age x, "α" and "β" are arbitrary constants, and "γ" is a constant representing age-independent mortality. The term "αe^βx" is known as the "Gompertz function" while "γ" is known as the "Makeham term" of the equation.

Usage

The Gompertz-Makeham law of mortality is used even in modern times by insurance companies to model expected adult lifetimes, as it gives fairly accurate death rates for human populations between the ages of 30 and 80. It should be noted, however, that at more advanced ages human death rates cease to increase as quickly as it predicts. It can also be used to predict death rates for species besides humans, though there are species to which it does not apply, and it does not necessarily describe mortality for child, infant, or extremely elderly individuals in those species for which it applies. In addition, several studies have found incidence curves of certain cancers to be nearly parallel to the Gompertz function, suggesting that they, and perhaps some other pathologies, depend on intrinsic aging processes. Researchers working with the University of Groningen have suggested using such similarities to distinguish between mainly intrinsically aging-associated and extrinsically caused mortality.

The Gompertz Law as an intrinsic principle of aging

The neatness and simplicity of the Gompertz law (the original, simpler version of the Gompertz-Makeham law of mortality) has prompted some researchers to speculate that it is a fundamental law of nature, akin to some of the laws of physics. For example, when it is written as m_t = S_tkce^kt, where m_t is the mortality rate, S_t is the proportion of survivors of the original population, and k and c are free parameters, researchers working with the University of Groningen have suggested that k and c may represent biological characteristics. They suggest that the parameter "k" might represent the accumulation of random damage or perturbations, while "c" might represent the vitality of an organism.

Gompertz models

Mortality in people with diabetes

Data analysis of all statutory health-insured persons (more than 47 million observations, of which over 6 million have diabetes) in in Germany in 2013 shows that mortality in people with diabetes constantly rises by 8.3% for males and 10.2% for females each year from the age of 30 (age range 30– > 95 years) and the probability that a person with diabetes dies before a person without diabetes is 61.9% for females and 63.3% for males. The survival information of the population with diabetes during a large part of the lifespan can thus be reduced to the two parameters of the Gompertz distribution.